
from an earlier study, that overall weight gain is unlikely). Usually, we conduct a two-tailed test since there is a risk that the program might actual result in weight gain rather than loss, but for this example, we will conduct a one-tailed test (perhaps because we have evidence, e.g. We judge the program to be effective if there is some weight loss at the 95% significance level. Can we conclude that the program is effective?Ī negative value in column B indicates that the subject gained weight. To test this claim 12 people were put on the program and the number of pounds of weight gain/loss was recorded for each person after two years, as shown in columns A and B of Figure 1.
The coefficient of skewness is relatively smallĮxample 1: A weight reduction program claims to be effective in treating obesity.The mean is approximately equal to the median.the median is in the center of the box and the whiskers extend equally in each direction The boxplot is relatively symmetrical i.e.The following are indications of symmetry: This can be determined by graphing the data. It turns out that the t distribution provides good results even when the population is not normal and even when the sample is small, provided the sample data is reasonably symmetrically distributed about the sample mean.

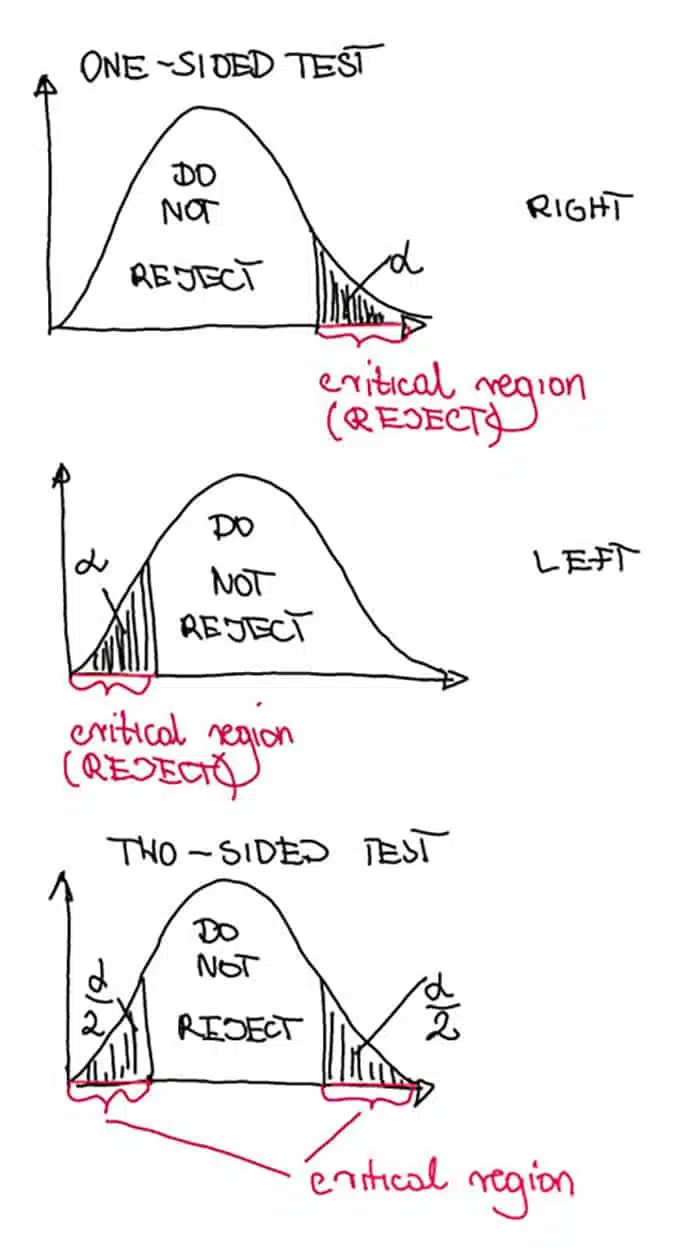
The t distribution provides a good way to perform one-sample tests on the mean when the population variance is not known provided the population is normal or the sample is sufficiently large so that the Central Limit Theorem applies (see Theorem 1 and Corollary 1 of Basic Concepts of t Distribution).


 0 kommentar(er)
0 kommentar(er)
